5.3 Recursive Data🔗

In Telling Apart Variants of Conditional Data, we used cases to distinguish between different forms of conditional data. We had used cases earlier, specifically to distinguish between empty and non-empty lists in Processing Lists. This suggests that lists are also a form of conditional data, just one that is built into Pyret. Indeed, this is the case.

To understand lists as conditional data, let’s create a data definition for a new type NumList which contains a list of numbers (this differs from built-in lists, which work with any type of element). To avoid conflicts with Pyret’s built-in empty value and link operator, we’ll have NumList use nl-empty as its empty value and nl-link as the operator that builds new lists. Here’s a partial definition:

data NumList:
  | nl-empty
  | nl-link( _________ )
end

Do Now!

Fill in the blank in the nl-link condition with the corresponding field(s) and corresponding types. The blank could contain anywhere from 0 through multiple fields.

From working with lists earlier, hopefully you remembered that list constructors take two inputs: the first element of the list and a list to build on (the rest of the list). That suggests that we need two fields here:

data NumList:
  | nl-empty
  | nl-link(first :: _________, rest :: _________ )
end

Do Now!

Fill in the types for first and rest if you haven’t already.

Since we’re making a list of numbers, the first field should contain type Number. What about the rest field? It needs to be a list of numbers, so its type should be NumList.

data NumList:
  | nl-empty
  | nl-link(first :: Number, rest :: NumList)
end

Notice something interesting (and new) here: the type of the rest field is the same type (NumList) as the conditional data that we are defining. We can, quite literally, draw the arrows that show the self-referential part of the definition:

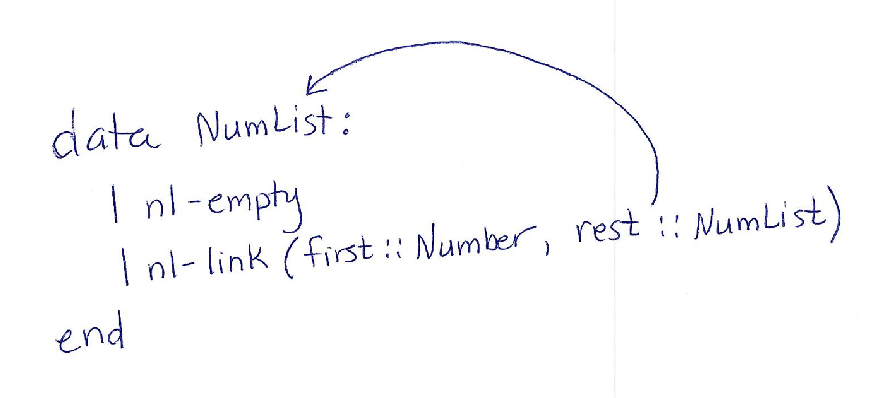
Does that actually work? Yes. Think about how we might build up a list with the numbers 2, 7, and 3 (in that order). We start with nl-empty, which is a valid NumList. We then use nl-link to add the numbers onto that list, as follows:

nl-empty
nl-link(3, nl-empty)
nl-link(7, nl-link(3, nl-empty))
nl-link(2, nl-link(7, nl-link(3, nl-empty)))

In each case, the rest argument is itself a valid NumList. While defining data in terms of itself might seem problematic, it works fine because in order to build actual data, we had to start with the nl-empty condition, which does not refer to NumList.

Data definitions that build on fields of the same type are called recursive data. Recursive data definitions are powerful because they permit us to create data that are unbounded or arbitrarily-sized. Given a NumList, there is an easy way to make a new, larger one: just use nl-link. So, we need to consider larger lists:

nl-link(1,
  nl-link(2,
    nl-link(3,
      nl-link(4,
        nl-link(5,
          nl-link(6,
            nl-link(7,
              nl-link(8,
                nl-empty))))

5.3.1 Functions to Process Recursive Data🔗

Let’s try to write a function contains-3, which returns true if the NumList contains the value 3, and false otherwise.

First, our header:

fun contains-3(nl :: NumList) -> Boolean:
  doc: "Produces true if the list contains 3, false otherwise"
end

Next, some tests:

fun contains-3(nl :: NumList) -> Boolean:
  doc: "Produces true if the list contains 3, false otherwise"
where:
  contains-3(nl-empty) is false
  contains-3(nl-link(3, nl-empty)) is true
  contains-3(nl-link(1, nl-link(3, nl-empty))) is true
  contains-3(nl-link(1, nl-link(2, nl-link(3, nl-link(4, nl-empty))))) is true
  contains-3(nl-link(1, nl-link(2, nl-link(5, nl-link(4, nl-empty))))) is false
end

As we did in Processing Fields of Variants, we will use cases to distinguish the variants. In addition, since we are going to have to use the fields of nl-link to compute a result in that case, we will list those in the initial code outline:

fun contains-3(nl :: NumList) -> Boolean:
  doc: "Produces true if the list contains 3, false otherwise"
  cases (NumList) nl:
    | nl-empty => ...
    | nl-link(first, rest) =>
      ... first ...
      ... rest ...
  end
end

Following our examples, the answer must be false in the nl-empty case. In the nl-link case, if the first element is 3, we’ve successfully answered the question. That only leaves the case where the argument is an nl-link and the first element does not equal 3:

fun contains-3(nl :: NumList) -> Boolean:
  cases (NumList) nl:
    | nl-empty => false
    | nl-link(first, rest) =>
      if first == 3:
        true
      else:
        # handle rest here
      end
  end
end

Since we know rest is a NumList (based on the data definition), we can use a cases expression to work with it. This is sort of like filling in a part of the template again:

fun contains-3(nl :: NumList) -> Boolean:
  cases (NumList) nl:
    | nl-empty => false
    | nl-link(first, rest) =>
      if first == 3:
        true
      else:
        cases (NumList) rest:
          | nl-empty => ...
          | nl-link(first-of-rest, rest-of-rest) =>
            ... first-of-rest ...
            ... rest-of-rest ...
        end
      end
  end
end

If the rest was empty, then we haven’t found 3 (just like when we checked the original argument, nl). If the rest was a nl-link, then we need to check if the first thing in the rest of the list is 3 or not:

fun contains-3(nl :: NumList) -> Boolean:
  cases (NumList) nl:
    | nl-empty => false
    | nl-link(first, rest) =>
      if first == 3:
        true
      else:
        cases (NumList) rest:
          | nl-empty => false
          | nl-link(first-of-rest, rest-of-rest) =>
            if first-of-rest == 3:
              true
            else:
              # fill in here ...
            end
        end
      end
  end
end

Since rest-of-rest is a NumList, we can fill in a cases for it again:

fun contains-3(nl :: NumList) -> Boolean:
  cases (NumList) nl:
    | nl-empty => false
    | nl-link(first, rest) =>
      if first == 3:
        true
      else:
        cases (NumList) rest:
          | nl-empty => false
          | nl-link(first-of-rest, rest-of-rest) =>
            if first-of-rest == 3:
              true
            else:
              cases (NumList) rest-of-rest:
                | nl-empty => ...
                | nl-link(first-of-rest-of-rest, rest-of-rest-of-rest) =>
                  ... first-of-rest-of-rest ...
                  ... rest-of-rest-of-rest ...
              end
            end
        end
      end
  end
end

See where this is going? Not anywhere good. We can copy this cases expression as many times as we want, but we can never answer the question for a list that is just one element longer than the number of times we copy the code.

So what to do? We tried this approach of using another copy of cases based on the observation that rest is a NumList, and cases provides a meaningful way to break apart a NumList; in fact, it’s what the recipe seems to lead to naturally.

Let’s go back to the step where the problem began, after filling in the template with the first check for 3:

fun contains-3(nl :: NumList) -> Boolean:
  cases (NumList) nl:
    | nl-empty => false
    | nl-link(first, rest) =>
      if first == 3:
        true
      else:
        # what to do with rest?
      end
  end
end

We need a way to compute whether or not the value 3 is contained in rest. Looking back at the data definition, we see that rest is a perfectly valid NumList, simply by the definition of nl-link. And we have a function (or, most of one) whose job is to figure out if a NumList contains 3 or not: contains-3. That ought to be something we can call with rest as an argument, and get back the value we want:

fun contains-3(nl :: NumList) -> Boolean:
  cases (NumList) nl:
    | nl-empty => false
    | nl-link(first, rest) =>
      if first == 3:
        true
      else:
        contains-3(rest)
      end
  end
end

And lo and behold, all of the tests defined above pass. It’s useful to step through what’s happening when this function is called. Let’s look at an example:

contains-3(nl-link(1, nl-link(3, nl-empty)))

First, we substitute the argument value in place of nl everywhere it appears; that’s just the usual rule for function calls.

=>  cases (NumList) nl-link(1, nl-link(3, nl-empty)):
       | nl-empty => false
       | nl-link(first, rest) =>
         if first == 3:
           true
         else:
           contains-3(rest)
         end
     end

Next, we find the case that matches the constructor nl-link, and substitute the corresponding pieces of the nl-link value for the first and rest identifiers.

=>  if 1 == 3:
      true
    else:
      contains-3(nl-link(3, nl-empty))
    end

Since 1 isn’t 3, the comparison evaluates to false, and this whole expression evaluates to the contents of the else branch.

=>  if false:
      true
    else:
      contains-3(nl-link(3, nl-empty))
    end

=>  contains-3(nl-link(3, nl-empty))

This is another function call, so we substitute the value nl-link(3, nl-empty), which was the rest field of the original input, into the body of contains-3 this time.

=>  cases (NumList) nl-link(3, nl-empty):
      | nl-empty => false
      | nl-link(first, rest) =>
        if first == 3:
          true
        else:
          contains-3(rest)
        end
    end

Again, we substitute into the nl-link branch.

=>  if 3 == 3:
      true
    else:
      contains-3(nl-empty)
    end

This time, since 3 is 3, we take the first branch of the if expression, and the whole original call evaluates to true.

=>  if true:
      true
    else:
      contains-3(nl-empty)
    end

=> true

An interesting feature of this trace through the evaluation is that we reached the expression contains-3(nl-link(3, nl-empty)), which is a normal call to contains-3; it could even be a test case on its own. The implementation works by doing something (checking for equality with 3) with the non-recursive parts of the datum, and combining that result with the result of the same operation (contains-3) on the recursive part of the datum. This idea of doing recursion with the same function on self-recursive parts of the datatype lets us extend our template to handle recursive fields.

5.3.2 A Template for Processing Recursive Data🔗

Stepping back, we have actually derived a new way to approach writing functions over recursive data. Back in Processing Lists, we had you write functions over lists by writing a sequence of related examples, using substitution across examples to derive a program that called the function on the rest of the list. Here, we are deriving that structure from the shape of the data itself.

In particular, we can develop a function over recursive data by breaking a datum into its variants (using cases), pulling out the fields of each variant (by listing the field names), then calling the function itself on any recursive fields (fields of the same type). For NumList, these steps yield the following code outline:

#|
fun num-list-fun(nl :: NumList) -> ???:
  cases (NumList) nl:
    | nl-empty => ...
    | nl-link(first, rest) =>
      ... first ...
      ... num-list-fun(rest) ...
  end
end
|#

We refer to this code outline as a template. Every data definition has a corresponding template which captures how to break a value of that definition into cases, pull out the fields, and use the same function to process any recursive fields.

Strategy: Writing a Template for Recursive Data

Given a recursive data definition, use the following steps to create the (reusable) template for that definition:

1. Create a function header (using a general-purpose placeholder name if you aren’t yet writing a specific function).

2. Use cases to break the recursive-data input into its variants.

3. In each case, list each of its fields in the answer portion of the case.

4. Call the function itself on any recursive fields.

The power of the template lies in its universality. If you are asked to write a specific function (such as contains-3) over recursive data (NumList), you can reproduce or copy (if you already wrote it down) the template, replace the generic function name in the template with the one for your specific function, then fill in the ellipses to finish the function.

When you see a recursive data definition (of which there will be many when programming in Pyret), you should naturally start thinking about what the recursive calls will return and how to combine their results with the other, non-recursive pieces of the datatype.

You have now seen two approaches to writing functions on recursive data: working out a sequence of related examples and modifying the template. Both approaches get you to the same final function. The power of the template, however, is that it scales to more complicated data definitions (where writing examples by hand would prove tedious). We will see examples of this as our data get more complex in coming chapters.

5.3.3 The Design Recipe🔗

We’ve showed you many techniques to use while designing programs, including developing examples, writing tests, and now writing and using data templates. Putting the pieces together yields a design recipe, adapted from that in How to Design Programs, that we can follow for designing recursive functions.

Strategy: The Design Recipe

Given a programming problem over recursive data:

1. Create a function header, including the function name and contract. The name will be necessary to make recursive calls, while the contract guides the design of the body.

2. Aided by the contract, which tells you what kind of data to consume and produce, write several illustrative examples of the function’s input and outputs, using concrete data. Include examples in which the input data of one extends the input data of another. This will later help you fill in the function.

3. The function’s contract tells you what kind of data you are processing. From the definition of the data, write out the template for it.

4. Adapt this template to the computation required by this specific problem. Use your examples to figure out how to fill in each case. You should have written an example for each case of data in the template. This is also where writing examples where input extended the other helps: the difference in output becomes the function body. See the several examples of this in Processing Lists.

5. Run your examples to make sure your function behaves as you expect.

6. Now start writing more fine-grained tests to confirm that you should be confident in your function. In particular, while the examples (which were written before you wrote the body of the function) focus on the expected “input-output” behavior, now that you have a concrete implementation, you should write tests that focus on its details.

Exercise

Use the design recipe to write a function contains-n that takes a NumList and a Number, and returns whether that number is in the NumList.

Exercise

Use the design recipe to write a function sum that takes a NumList, and returns the sum of all the numbers in it. The sum of the empty list is 0.

Exercise

Use the design recipe to write a function remove-3 that takes a NumList, and returns a new NumList with any 3’s removed. The remaining elements should all be in the list in the same order they were in the input.

Exercise

Write a data definition called NumListList that represents a list of NumLists, and use the design recipe to write a function sum-of-lists that takes a NumListList and produces a NumList containing the sums of the sub-lists.

Exercise

Write a data definition and corresponding template for StrList, which captures lists of strings.