4.1 Introduction to Tabular Data🔗

Do Now!

Can you come up with more examples?

Exercise

Find the characteristics of tabular data in the other examples described above, as well as in the ones you described.

We will now learn how to program with tables and to think about decomposing tasks involving them.You can also look up the full Pyret documentation for table operations. The programs later in this chapter use a function-based notation for processing tables, which you can access via the following:

include shared-gdrive(
  "dcic-2021",
  "1wyQZj_L0qqV9Ekgr9au6RX2iqt2Ga8Ep")

Documentation on the function-based table operators is available on a separate page outside of the Pyret documentation.

4.1.1 Creating Tabular Data🔗

table: name, age
  row: "Alicia", 30
  row: "Meihui", 40
  row: "Jamal", 25
end

Exercise

Change different parts of the above example—e.g., remove a necessary value from a row, add an extraneous one, remove a comma, add an extra comma, leave an extra comma at the end of a row—and see what errors you get.

check:
  table: name, age
    row: "Alicia", 30
    row: "Meihui", 40
    row: "Jamal", 25
  end
  is-not
  table: age, name
    row: 30, "Alicia"
    row: 40, "Meihui"
    row: 25, "Jamal"
  end
end

The check: annotation here is a way of writing is assertions about expressions outside of the context of a function (and its where block). We’ll learn more about check in From Examples to Tests.

people = table: name, age
  row: "Alicia", 30
  row: "Meihui", 40
  row: "Jamal", 25
end

With tables, we begin to explore data that contain other (smaller) pieces of data. We’ll refer to such data as structured data. Structured data organize their inner data in a structured way (here, rows and columns). As with images, when we wrote code that reflected the structure of the final image, we will see that code that works with tables also follows the structure of the data.

4.1.2 Extracting Rows and Cell Values🔗

Given a table, we sometimes want to look up the value of a particular cell. We’ll work with the following table showing the number of riders on a shuttle service over several months:

shuttle = table: month, riders
  row: "Jan", 1123
  row: "Feb", 1045
  row: "Mar", 1087
  row: "Apr", 999
end

Do Now!

If you put this table in the definitions pane and press Run, what will be in the Pyret directory once the interactions prompt appears? Would the column names be listed in the directory?

As a reminder, the directory contains only those names that we assign values to using the form name = . The directory here would contain shuttle, which would be bound to the table (yes, the entire table would be in the directory!). The column names would not have their own entries in the directory. If we did try to put a column name in the directory, which value would it map to? There is a different value in the column for every row. Names in the directory map to only one value.

Let’s explore how to extract the value of a given cell (row and column) in the table. Concretely, assume we want to extract the number of riders in March (1087) so we can use it in another computation. How do we do that?

Pyret (and most other programming languages designed for data analysis) organizes tables as collections of rows with shared columns. Given that organization, we get to a specific cell by first isolating the row we are interested in, then retrieving the contents of the cell.

shuttle.row-n(2)

If we run this expression at the prompt, we get

This is a new type of data called a Row. When Pyret displays a Row value, it shows you the column names and the corresponding values within the row.

To extract the value of a specific column within a row, we write the row followed by the name of the column (as a string) in square brackets. Here are two equivalent ways of getting the value of the riders column from the row for March:

shuttle.row-n(2)["riders"]

march-row = shuttle.row-n(2)
march-row["riders"]

Do Now!

What names would be in the Pyret directory when using each of these approaches?

Once we have the cell value (here a Number), we can use it in any other computation, such as

shuttle.row-n(2)["riders"] >= 1000

Do Now!

What do you expect would happen if you forgot the quotation marks and instead wrote:

shuttle.row-n(2)[riders]

What would Pyret do and why?

4.1.3 Functions over Rows🔗

Now that we have the ability to isolate Rows from tables, we can write functions that ask questions about individual rows. We just saw an example of doing a computation over row data, when we checked whether the row for March had more than 1000 riders. What if we wanted to do this comparison for an arbitrary row of this table? Let’s write a function! We’ll call it cleared-1K.

Let’s start with a function header and some examples:

fun cleared-1K(r :: Row) -> Boolean:
  doc: "determine whether given row has at least 1000 riders"
  ...
where:
  cleared-1K(shuttle.row-n(2)) is true
  cleared-1K(shuttle.row-n(3)) is false
end

To fill in the body of the function, we extract the content of the "riders" cell and compare it to 1000:

fun cleared-1K(r :: Row) -> Boolean:
  doc: "determine whether given row has at least 1000 riders"
  r["riders"] >= 1000
where:
  cleared-1K(shuttle.row-n(2)) is true
  cleared-1K(shuttle.row-n(3)) is false
end

Do Now!

Looking at the examples, both of them share the shuttle.row-n portion. Would it have been better to instead make cleared-1K a function that takes just the row position as input, such as:

fun cleared-1K(row-pos :: Number) -> Boolean:
  ...
where:
  cleared-1K(2) is true
  cleared-1K(3) is false
end

What are the benefits and limitations to doing this?

In general, the version that takes the Row input is more flexible because it can work with a row from any table that has a column named "riders". We might have another table with more columns of information or different data tables for different years. If we modify cleared-1K to only take the row position as input, that function will have to fix which table it works with. In contrast, our original version leaves the specific table (shuttle) outside the function, which leads to flexibility.

Exercise

Write a function is-winter that takes a Row with a "month" column as input and produces a Boolean indicating whether the month in that row is one of "Jan", "Feb", or "Mar".

Exercise

Write a function low-winter that takes in Row with both "month" and "riders" columns and produces a Boolean indicating whether the row is a winter row with fewer than 1050 riders.

Exercise

Practice with the program directory! Take a Row function and one of its where examples, and show how the program directory evolves as you evaluate the example.

4.1.4 Processing Rows🔗

So far, we have looked at extracting individual rows by their position in the table and computing over them. Extracting rows by position isn’t always convenient: we might have hundreds or thousands of rows, and we might not know where the data we want even is in the table. We would much rather be able to write a small program that identifies the row (or rows!) that meets a specific criterion.

Pyret offers three different notations for processing tables: one uses functions, one uses methods, and one uses a SQL-like notation. This chapter uses the function-based notation. The SQL-like notation and the methods-based notation are shown in the Pyret Documentation. To use the function-based notation, you’ll need to include the file specified in the main narrative.

The rest of this section assumes that you have loaded the functions notation for working with tables, using the following line in your Pyret file:

include shared-gdrive(
  "dcic-2021",
  "1wyQZj_L0qqV9Ekgr9au6RX2iqt2Ga8Ep")

4.1.4.1 Finding Rows🔗

Imagine that we wanted to write a program to locate a row that has fewer than 1000 riders from our shuttle table. With what we’ve studied so far, how might we try to write this? We could imagine using a conditional, like follows:

if shuttle.row-n(0)["riders"] < 1000:
  shuttle.row-n(0)
else if shuttle.row-n(1)["riders"] < 1000:
  shuttle.row-n(1)
else if shuttle.row-n(2)["riders"] < 1000:
  shuttle.row-n(2)
else if shuttle.row-n(3)["riders"] < 1000:
  shuttle.row-n(3)
else: ... # not clear what to do here
end

Do Now!

What benefits and limitations do you see to this approach?

There are a couple of reasons why we might not care for this solution. First, if we have thousands of rows, this will be terribly painful to write. Second, there’s a lot of repetition here (only the row positions are changing). Third, it isn’t clear what to do if there aren’t any matching rows. In addition, what happens if there are multiple rows that meet our criterion? In some cases, we might want to be able to identify all of the rows that meet a condition and use them for a subsequent computation (like seeing whether some months have more low-ridership days than others).

This conditional is, however, the spirit of what we want to do: go through the rows of the table one at a time, identifying those that match some criterion. We just don’t want to be responsible for manually checking each row. Fortunately for us, Pyret knows how to do that. Pyret knows which rows are in a given table. Pyret can pull out those rows one position at a time and check a criterion about each one.

We just need to tell Pyret what criterion we want to use.

As before, we can express our criterion as a function that takes a Row and produces a Boolean (a Boolean because our criterion was used as the question part of an if expression in our code sketch). In this case, we want:

fun below-1K(r :: Row) -> Boolean:
  doc: "determine whether row has fewer than 1000 riders"
  r["riders"] < 1000
where:
  below-1K(shuttle.row-n(2)) is false
  below-1K(shuttle.row-n(3)) is true
end

Now, we just need a way to tell Pyret to use this criterion as it searches through the rows. We do this with a function called filter-with which takes two inputs: the table to process and the criterion to check on each row of the table:

filter-with(shuttle, below-1K)

Under the hood, filter-with works roughly like the if statement we outlined above: it takes each row one at a time and calls the given criterion function on it. But what does it do with the results?

filter-with(shuttle, is-winter)

winter = filter-with(shuttle, is-winter)

4.1.4.2 Ordering Rows🔗

Let’s ask a new question: which winter month had the fewest number of riders?. This question requires us to identify a specific row, namely, the winter row with the smallest value in the "riders" column.

Do Now!

Can we do this with filter-with? Why or why not?

Think back to the if expression that motivated filter-with: each row is evaluated independently of the others. Our current question, however, requires comparing across rows. That’s a different operation, so we will need more than filter-with.

Tools for analyzing data (whether programming languages or spreadsheets) provide ways for users to sort rows of a table based on the values in a single column. That would help us here: we could sort the winter rows from smallest to largest value in the "riders" column, then extract the "riders" value from the first row. First, let’s sort the rows:

order-by(winter, "riders", true)

The order-by function takes three inputs: the table to sort (winter), the column to sort on ("riders"), and a Boolean to indicate whether we want to sort in increasing order. (Had the third argument been false, the rows would be sorted in decreasing order of the values in the named column.)

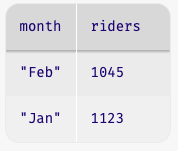
In the sorted table, the row with the fewest riders is in the first position. Our original question asked us to lookup the month with the fewest riders. We did this earlier.

Do Now!

Write the code to extract the name of the winter month with the fewest riders.

Here are two ways to write that computation:

order-by(winter, "riders", true).row-n(0)["month"]

sorted = order-by(winter, "riders", true)
least-row = sorted.row-n(0)
least-row["month"]

Do Now!

Which of these two ways do you prefer? Why?

Do Now!

How does each of these programs affect the program directory?

Note that this problem asked us to combine several actions that we’ve already seen on rows: we identify rows from within a table (filter-with), order the rows (order-by), extract a specific row (row-n), then extract a cell (with square brackets and a column name). This is typical of how we will operate on tables, combining multiple operations to compute a result (much as we did with programs that manipulate images).

4.1.4.3 Adding New Columns🔗

employees =
  table: name,   hourly-wage, hours-worked
    row: "Harley",  15,          40
    row: "Obi",     20,          45
    row: "Anjali",  18,          39
    row: "Miyako",  18,          40
  end

employees =
  table: name, hourly-wage, hours-worked, total-wage
    row: "Harley", 15,         40,         15 * 40
    row: "Obi",    20, 	       45,         20 * 45
    row: "Anjali", 18, 	       39,         18 * 39
    row: "Miyako", 18, 	       40,         18 * 40
  end

Previously, when we have had a computation that we performed multiple times, we created a helper function to do the computation.

Do Now!

Propose a helper function for computing total wages given the hourly wage and number of hours worked.

Perhaps you came up with something like:

fun compute-wages(wage :: Number, hours :: Number) -> Number:
  wage * hours
end

employees =
  table: name, hourly-wage, hours-worked, total-wage
    row: "Harley", 15, 40, compute-wages(15, 40)
    row: "Obi",    20, 45, compute-wages(20, 45)
    row: "Anjali", 18, 39, compute-wages(18, 39)
    row: "Miyako", 18, 40, compute-wages(18, 40)
  end

This is the right idea, but we can actually have this function do a bit more work for us. The wage and hours values are in cells within the same row. So if we could instead get the current row as an input, we could write:

fun compute-wages(r :: Row) -> Number:
  r["hourly-wage"] * r["hours-worked"]
end

employees =
  table: name, hourly-wage, hours-worked, total-wage
    row: "Harley", 15, 40, compute-wages(<row0>)
    row: "Obi",    20, 45, compute-wages(<row1>)
    row: "Anjali", 18, 39, compute-wages(<row2>)
    row: "Miyako", 18, 40, compute-wages(<row3>)
  end

But now, we are writing calls to compute-wages over and over! Adding computed columns is a sufficiently common operation that Pyret provides a table function called build-column for this purpose. We use it by providing the function to use to populate values in the new column as an input:

fun compute-wages(r :: Row) -> Number:
  doc: "compute total wages based on wage and hours worked"
  r["hourly-wage"] * r["hours-worked"]
end

build-column(employees, "total-wage", compute-wages)

4.1.4.4 Calculating New Column Values🔗

Sometimes, we just want to calculate new values for an existing column, rather than create an entirely new column. Giving raises to employees is one such example. Assume we wanted to give a 10% raise to all employees making less than 20 an hour. We could write:

fun new-rate(rate :: Number) -> Number:
  doc: "Raise rates under 20 by 10%"
  if rate < 20:
    rate * 1.1
  else:
    rate
  end
where:
  new-rate(20) is 20
  new-rate(10) is 11
  new-rate(0) is 0
end

fun give-raises(t :: Table) -> Table:
  doc: "Give a 10% raise to anyone making under 20"
  transform-column(t, "hourly-wage", new-rate)
end

Do Now!

Run give-raises on the employees table. What wage will show for "Miyako" in the employees table after give-raises completes. Why?

Like all other Pyret Table operations, transform-column produces a new table, leaving the original intact. Editing the original table could be problematic–what if you made a mistake? How would you recover the original table in that case? In general, producing new tables with any modifications, then creating a new name for the updated table once you have the one you want, is a less error-prone way of working with datasets.

4.1.5 Examples for Table-Producing Functions🔗

How do we write examples for functions that produce tables? Conceptually, the answer is simply "make sure you got the output table that you expected". Logistically, writing examples for table functions seems more painful because writing out an expected output tables is more work than simply writing the output of a function that produces numbers or strings. What can we do to manage that complexity?

Do Now!

How might you write the where block for give-raises?

Here are some ideas for writing the examples practically:

• Simplify the input table. Rather than work with a large table with all of the columns you have, create a small table that has sufficient variety only in the columns that the function uses. For our example, we might use:

  wages-test =
    table: hourly-wage
      row: 15
      row: 20
      row: 18
      row: 18
    end

  Do Now!

  Would any table with a column of numbers work here? Or are there some constraints on the rows or columns of the table?

  The only constraint is that your input table has to have the column names used in your function.

• Remember that you can write computations in the code to construct tables. This saves you from doing calculations by hand.

  where:
    give-raises(wages-test) is
    table: hourly-wage
      row: 15 * 1.1
      row: 20
      row: 18 * 1.1
      row: 18 * 1.1
    end

  This example shows that you can write an output table directly in the where: block – the table doesn’t need to be named outside the function.

• Create a new table by taking rows from an existing table. If you were instead writing examples for a function that involves filtering out rows of a table, it helps to know how to create a new table using rows of an existing one. For example, if we were writing a function to find all rows in which employees were working exactly 40 hours, we’d like to make sure that the resulting table had the first and fourth rows of the employees table. Rather than write a new table expression to create that table, we could write it as follows:

  emps-at-40 =
    add-row(
      add-row(employees.empty(),
        employees.row-n(0)),
      employees.row-n(3))

  Here, employees.empty() creates a new, empty table with the same column headers as employees. We’ve already seen how row-n extracts a row from a table. The add-row function places the given row at the end of the given table.

Another tip to keep in mind: when the only thing your function does is call a built-in function like transform-column it usually suffices to write examples for the function you wrote to compute the new column value. It is only when your code is combining table operations, or doing more complex processing than a single call to a built-in table operation that you really need to present your own examples to a reader of your code.